Su LinkedIn il professore Massimiliano Politano, docente aggregato presso l’Università degli Studi di Napoli Federico II e studioso di discipline quantitative applicate all’economia e alla finanza, ha pubblicato un post volto a chiarire una polemica nata attorno a una frase attribuita al magistrato Nicola Gratteri nel contesto del dibattito referendario.
La frase al centro della discussione era “i delinquenti votano Sì”. Una parte del pubblico ha interpretato quell’affermazione come se implicasse che a votare Sì fossero esclusivamente delinquenti. Da qui sono nate reazioni indignate e accuse di generalizzazione offensiva nei confronti di un intero elettorato.

Politano interviene su Linkedin non sul piano politico ma su quello logico. Il suo punto è che tra le due frasi “i delinquenti votano Sì” e “solo i delinquenti votano Sì” esiste una differenza strutturale netta. La prima è un’affermazione inclusiva: indica che esiste un sottoinsieme di delinquenti che vota Sì. Non dice nulla sulla totalità dei votanti Sì. La seconda è un’affermazione esclusiva: sostiene che chiunque voti Sì appartenga necessariamente alla categoria dei delinquenti. Sono due proposizioni con contenuti logici distinti e non equivalenti.
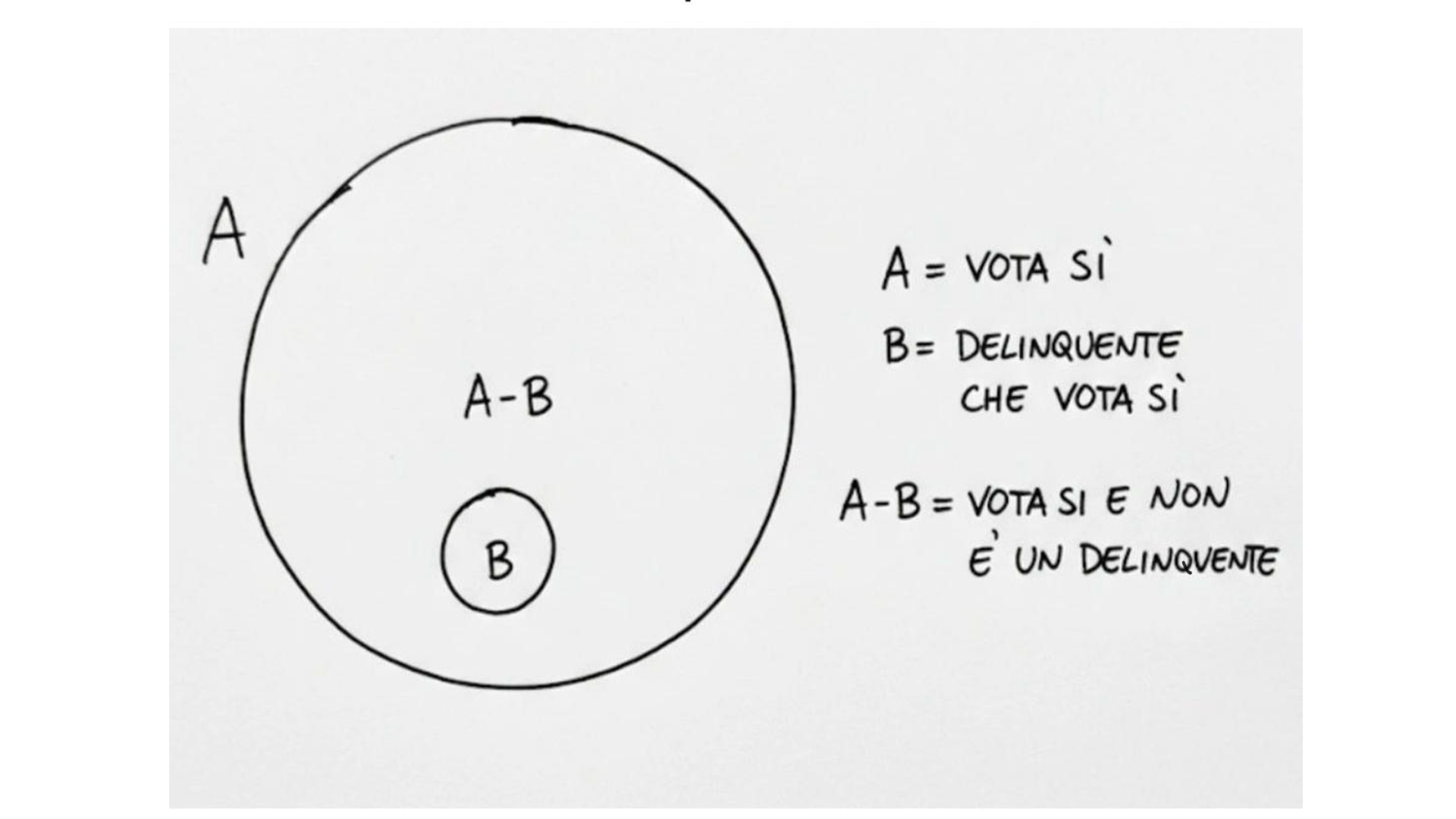
Per rendere evidente questa differenza, il professore allega un diagramma di Venn. Nel disegno compare un grande cerchio indicato con la lettera A che rappresenta l’insieme di chi vota Sì. All’interno di questo cerchio è tracciato un cerchio più piccolo indicato con la lettera B che rappresenta i delinquenti che votano Sì. La parte del cerchio grande che non è occupata dal cerchio piccolo, cioè l’area A meno B, rappresenta chi vota Sì ma non è un delinquente.
Il punto è matematicamente semplice. Affermare che “solo i delinquenti votano Sì” significherebbe che l’insieme A coincide interamente con l’insieme B. In termini insiemistici, l’area A meno B dovrebbe essere vuota. Nel diagramma, invece, quell’area esiste. Questo dimostra che la prima affermazione non implica la seconda.
Il post di Politano è richiamo alla precisione logica. Non entra nel merito della posizione politica, ma evidenzia come una lettura imprecisa delle parole possa trasformare un’asserzione descrittiva in un’accusa generalizzata che, sul piano formale, non è contenuta nella frase originaria.